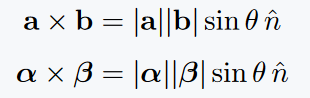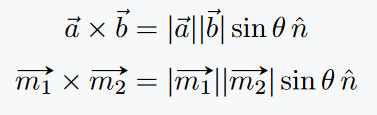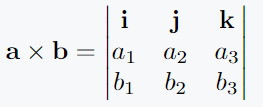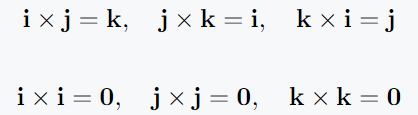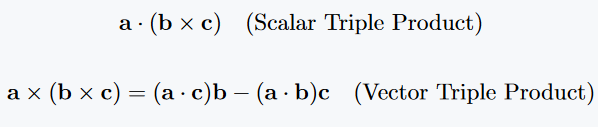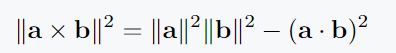Imagine you want to show the multiplication of two vectors using LaTeX, just like in a math textbook or research paper.
In this guide, we will explain how to write the product of two vectors in LaTeX. We will show you which commands to use and how to set it up nicely.
Basic syntax of cross product
It is important to know the correct syntax for multiplying vectors in LaTeX. Vectors are usually written in two ways: in bold or with an arrow on top. Let us look at both methods.
Bold vectors
You can write vectors in bold using the \mathbf{} command. If you use symbols and want them in bold, sometimes you need the \boldsymbol{} command.
\[ \mathbf{a} \times \mathbf{b} \]
\[ \boldsymbol{\alpha} \times \boldsymbol{\beta} \]
Output:
Arrowed vectors
If you prefer to show vectors with an arrow on top, use the \vec{} command. Sometimes the arrow made by \vec{} can look small. In that case, you can use the esvect package with its \vv{} command, which gives a larger arrow.
\documentclass{article}
\usepackage{esvect}
\begin{document}
\[ \vec{a} \times \vec{b} \]
\[ \vv{m_1} \times \vv{m_2} \]
\end{document}Output:
Both methods work well, and you can choose the style that best fits your work.
Matrix Form of the Vector Product
Sometimes, you need to show the multiplication using a matrix, written as a determinant. For example, if a = [a1,a2,a3] and b = [b1,b2,b3], you can write:
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[
\mathbf{a} \times \mathbf{b} = \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3 \\
\end{vmatrix}
\]
\end{document}Output:
Here, the vmatrix environment creates a 3×3 matrix. The symbols \mathbf{i}, \mathbf{j}, and \mathbf{k} represent the unit vectors along the x, y, and z axes.
Multiplication of Unit Vectors
It is useful to know how to multiply unit vectors. For example:
\[ \mathbf{i} \times \mathbf{j} = \mathbf{k}, \quad
\mathbf{j} \times \mathbf{k} = \mathbf{i}, \quad
\mathbf{k} \times \mathbf{i} = \mathbf{j} \]
\[ \mathbf{i} \times \mathbf{i} = \mathbf{0}, \quad
\mathbf{j} \times \mathbf{j} = \mathbf{0}, \quad
\mathbf{k} \times \mathbf{k} = \mathbf{0} \]Output:
Key Properties of the Vector Operation
This type of vector product has several important properties. Here are a few examples:
\[ \mathbf{a} \times \mathbf{b} = - (\mathbf{b} \times \mathbf{a}) \quad \text{(Anticommutative Property)} \]
\[ \mathbf{a} \times (\mathbf{b} + \mathbf{c}) = \mathbf{a} \times \mathbf{b} + \mathbf{a} \times \mathbf{c} \quad \text{(Distributive Property)} \]
\[ (k\mathbf{a}) \times \mathbf{b} = k (\mathbf{a} \times \mathbf{b}) \quad \text{(Scalar Multiplication Property)} \]Output:
Triple Products
Next, we discuss three-element operations involving vectors. There are two types: the scalar triple product and the vector triple product.
\[ \mathbf{a} \cdot (\mathbf{b} \times \mathbf{c}) \quad \text{(Scalar Triple Product)} \]
\[ \mathbf{a} \times (\mathbf{b} \times \mathbf{c}) = (\mathbf{a} \cdot \mathbf{c})\mathbf{b} - (\mathbf{a} \cdot \mathbf{b})\mathbf{c} \quad \text{(Vector Triple Product)} \]Output:
Lagrange Identity
The Lagrange Identity shows the relationship between the squared magnitude of the vector multiplication and the dot product of two vectors.
\[ \|\mathbf{a} \times \mathbf{b}\|^2 = \|\mathbf{a}\|^2 \|\mathbf{b}\|^2 - (\mathbf{a} \cdot \mathbf{b})^2 \]
Output: