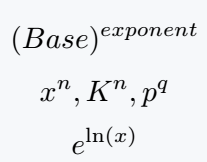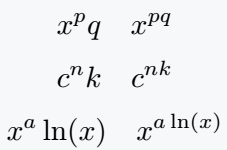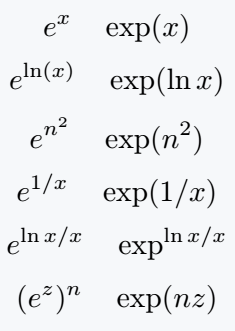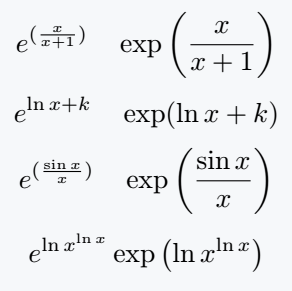Superscripts are essential for mathematical notation, particularly in exponentiation, where a base is raised to a power or exponent.
This is represented in LaTeX using the syntax base^{exponent}, producing expressions like xⁿ or aᵏ.
Basic syntax for superscripts
In LaTeX, exponents are written using the caret ^ symbol. If the exponent consists of more than one character, it must be enclosed in curly brackets {}.
\documentclass{article}
\begin{document}
\[ (Base)^{exponent} \]
\[ x^n,K^n,p^q \]
\[ e^{\ln(x)} \]
\end{document}Output :
Handling multi-character
If the exponent consists of multiple characters, it must be enclosed in curly brackets.
\documentclass{article}
\begin{document}
\[ x^pq \quad x^{pq} \]
\[ c^nk \quad c^{nk} \]
\[ x^a\ln (x) \quad x^{a\ln (x)} \]
\end{document}Output :
Exponential functions
There are two common ways to express exponential functions in LaTeX.
1. Using the mathematical constant e as the base.
2. Using the exp function.
LaTeX provides a predefined command for \exp, allowing for cleaner expressions in complex cases.
\documentclass{article}
\begin{document}
\[ e^x \quad \exp(x) \]
\[ e^{\ln(x)} \quad \exp(\ln x) \]
\[ e^{n^2} \quad \exp(n^2) \]
\[ e^{1/x} \quad \exp(1/x) \]
\[ e^{\ln x/x} \quad \exp^{\ln x/x} \]
\[ (e^z)^n \quad \exp(nz) \]
\end{document}Output :
Choosing between e^x and \exp(x)
Have you ever thought about why LaTeX has both e^x and \exp(x)? The reason is to make math easier to read and understand.
e^x is short and common, but \exp(x) is useful when the equation is more complex and might be confusing.
\documentclass{article}
\begin{document}
\[ e^{(\frac{x}{x+1})} \quad \exp\left(\frac{x}{x+1}\right) \]
\[ e^{\ln x +k} \quad \exp(\ln x + k) \]
\[ e^{(\frac{\sin x}{x})} \quad \exp\left(\frac{\sin x}{x}\right) \]
\[ e^{\ln x^{\ln x}} \exp\left(\ln x^{\ln x}\right) \]
\end{document}Output :
As seen in the output, using \exp() improves readability in fractions and nested exponents.
Continuous fractions
Exponential functions are often represented using continued fractions, which are best formatted using \cfrac{numerator}{denominator} instead of the standard \frac{} for better alignment.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[ e^x = 1+\cfrac{x}{1-\cfrac{x}{x+2 -\cfrac{2x}{x+3-\cfrac{3x}{x+4-\cfrac{4x}{\ddots}}}}} \]
\[ e^z = 1+\cfrac{2z}{2-z+\cfrac{z^2}{6 +\cfrac{z^2}{10+\cfrac{z^2}{14+\cfrac{z^2}{\ddots}}}}} \]
\end{document}Output :