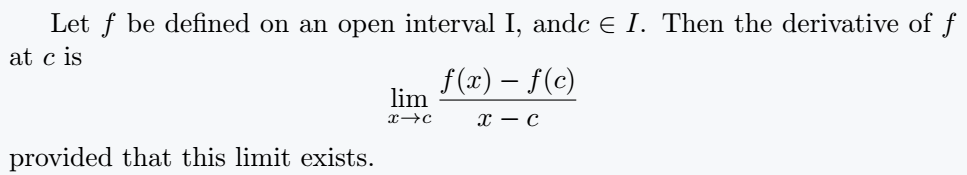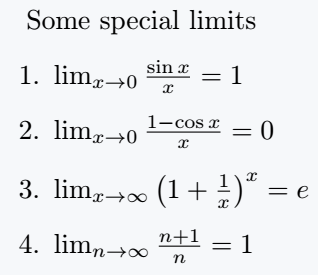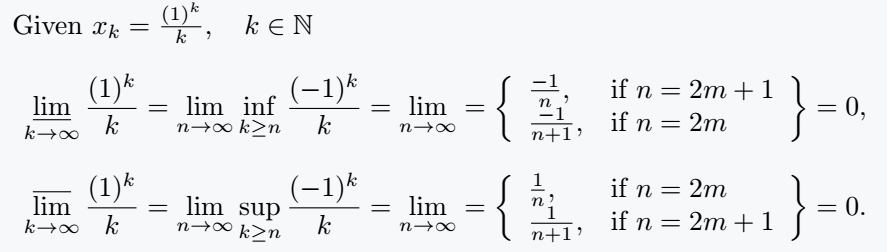How do you write limit in LaTeX?

Limit is an essential mathematical concept and LaTeX makes it very easy to write. Many learners get confused about using arrows, subscripts, and different variations of limit commands.

In this tutorial, you will find structured explanations with proper examples so that all doubts are cleared.

Basic Limit Command

The most basic command for limits in LaTeX is \lim. To make it meaningful, we usually attach a subscript and sometimes an arrow using \to.

\lim_{..\to..}

\lim: This produces the standard “lim” notation in math mode. It is the starting point of any limit expression.
_{..\to..}: This is a subscript showing the variable and its target value. The arrow \to represents “approaches”.

\documentclass{article}
\begin{document}
   A limit is the value that a function (or sequence) approaches as the input (or index) approaches some value. Suppose $ f $ is a real-valued function and $ \ell $ is a real number. Intuitively speaking, the expression
   \[\lim _{x \to \ell }f(x)=L  \]
   means that $ f(x) $ can be made to be as close to $ \ell $ as desired, by making $ x $ sufficiently close to $ \ell $
\end{document}

Output :

Variants of Limit Commands

LaTeX has multiple commands to represent different types of limits such as limsup, liminf, and projective or direct limits. These are very helpful in advanced mathematics.

Limits LaTeX commands	Output
`\lim`	lim
`\liminf`
`\limsup`	lim sup
`\varinjlim`
`\varprojlim`
`\varlimsup`
`\varliminf`
`\projlim`	proj lim

Limit Superior and Inferior

For sequences of numbers, \limsup and \liminf are used to describe the limit superior and limit inferior. They are very common in real analysis.

\limsup_{..\to..}
\liminf_{..\to..}

\limsup: This command represents the limit superior of a sequence. It is the largest subsequential limit.
\liminf: This command represents the limit inferior of a sequence. It is the smallest subsequential limit.

\documentclass{article}
\usepackage{amssymb}
\begin{document}
    Let $ (a_n)_{n \in \mathbb{N}} $ be a sequence of real numbers. We define 
    \begin{enumerate}
      \item Limit Superior denoted by $ \limsup  $ 
       \[ \limsup_{n \to \infty} a_n := \lim_{n \to \infty}(\sup\{a_n|k\geq n\}) \]
      \item Limit inferior denoted by $ \liminf  $
       \[ \liminf_{n \to \infty} a_n := \lim_{n \to \infty}(\inf\{a_n|k\geq n\}) \]
     \end{enumerate}
\end{document}

Output :

Other notations for \limsup and \liminf also include commands like \varinjlim, \varprojlim, and \projlim which are used for direct and inverse limits.

Examples of Limits

Examples help to clearly understand how different limit commands are used.

Example 1: Derivative definition using limit.

\documentclass{article}
\usepackage{amssymb}
\begin{document}
   Let $ f $ be defined on an open interval I, and$  c \in I $. Then the derivative of $ f $ at $ c $ is 
   \[ \lim_{x \to c}\frac{f(x) - f(c)}{x - c} \]
   provided that this limit exists.
\end{document}

Output :

Example 2: Special limits in calculus.

\documentclass{article}
\begin{document}
   Some special limits 
   \begin{enumerate}
    \item $ \lim_{x \to 0}\frac{\sin x}{x} = 1 $ 
    \item $  \lim_{x \to 0}\frac{1 - \cos x}{x} = 0 $ 
    \item $ \lim_{x \to \infty} \left(1  + \frac{1}{x}\right)^x = e  $
    \item $ \lim_{n \to \infty} \frac{n+1}{n} = 1 $
   \end{enumerate}
\end{document}

Output :

Example 3: Sequence with limsup and liminf.

\documentclass{article}
\usepackage{amssymb,mathtools}
\begin{document}
   Given $ x_k = \frac{(1)^k}{k}, \quad k \in \mathbb{N}  $
   \[\varliminf_{k \to \infty}  \frac{(1)^k}{k} = \lim_{n \to \infty}\inf_{k \geq n}\frac{(-1)^k}{k} = \lim_{n \to \infty} = \left\{ \begin{array}{ll}
   \frac{-1}{n}, & \text{if $ n = 2m+1 $}\\ 
   \frac{-1}{n+1}, & \text{if $ n = 2m $}
   \end{array}\right\} = 0, \] 
   \[ \varlimsup_{k \to \infty}  \frac{(1)^k}{k} = \lim_{n \to \infty}\sup_{k \geq n}\frac{(-1)^k}{k} = \lim_{n \to \infty} = \left\{ \begin{array}{ll}
   \frac{1}{n}, & \text{if $ n = 2m $}\\ 
   \frac{1}{n+1}, & \text{if $ n = 2m+1 $}
   \end{array}\right\} = 0. \]
\end{document}

Output :

Example 4: Projective and inductive limits.

\documentclass{article}
\usepackage{mathtools}
\begin{document}
   Given an inverse system $ ((A_{i})_{i \in I},(f_{ij})_{i\leq j\in I}) $ as a particular subgroup of the direct product of the $ A_{i} $'s, we define the inverse limit(the projective limit)
   \[ A=\varprojlim _{i\in I}{A_{i}}=\projlim _{i\in I}{A_{i}}= \left\{\left.{\vec{a}}\in \prod_{i\in I}A_{i}\;\right|\;a_{i}=f_{ij}(a_{j}){\text{for all }}i\leq j\; {\text{in}}\; I\right\}. \]
   Given a direct system $ \langle A_{i},f_{{ij}}\rangle $, The direct(inductive) limit denoted by  $ \varinjlim A_{i} $ and is defined as 
   \[ \varinjlim A_{i}=\bigsqcup _{i}A_{i}{\bigg /}\sim  \]			
   Its underlying set is the disjoint union of the $ A_{i} $\,'s modulo a certain equivalence relation $ \sim  $
\end{document}

Output :