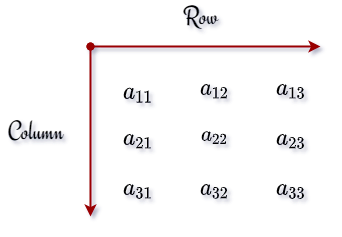
A matrix is an array and table where numbers, symbols, and expressions are arranged along the row and column according to the sequence. These numbers, symbols, and expressions are called its elements.
Before defining it in LaTeX, you need to understand its structure well.
Define matrix syntax
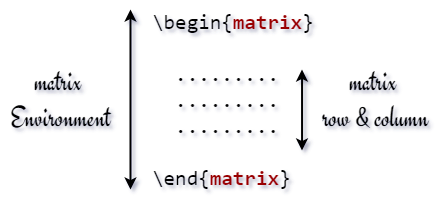
1. First, to define a matrix in LaTeX, you need to create an environment for it.
The matrix is passed as an argument between \begin and \end commands. This argument indicates that it will be bound by which bracket. So, there is more than one argument to define more than one bracket.
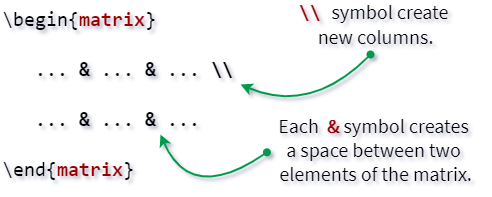
2. Second, you need to create rows and columns according to your needs.
The & and \\ symbols are used to organize elements systematically into rows and columns within an environment. The & symbol separates elements within a row, while the \\ symbol moves to the next row.
3. Third, the elements must be inserted sequentially into the environment. Which will be separated by the & symbol along the row.
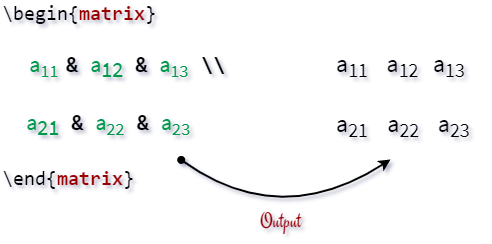
In latex, you can define a complete matrix with the help of the above three steps.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[
\begin{matrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{matrix}
\]
\end{document}Output :
The matrix is not specified by default in latex. For this, you need to install the external package amsmath.
Different types of brackets
The arranged elements are enclosed within different types of brackets, while some remain without any brackets. The choice of brackets depends on the specified argument.
Take a look at the table below to see the variations in formatting.
pmatrix |
( ) |
bmatrix |
[ ] |
Bmatrix |
{ } |
vmatrix |
| | |
Vmatrix |
|| || |
Without brackets
If elements are not enclosed within brackets, the appropriate argument must be specified within the environment to structure them properly.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[
\begin{matrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{matrix}
\]
\end{document}Output :
Use parenthesis
If enclosed within parentheses, use pmatrix as the argument.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[\begin{pmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{pmatrix}\]
\end{document}Output :
Use square bracket
If enclosed within square brackets, use bmatrix as the argument between the \begin and \end commands.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[\begin{bmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{bmatrix}\]
\end{document}Output :
Use curly bracket
Bmatrix should be used for curly brackets. LaTeX is case-sensitive, meaning uppercase and lowercase letters are treated differently. For example, Bmatrix and bmatrix are distinct arguments.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[\begin{Bmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{Bmatrix}\]
\end{document}Output :
Use vertical bars
You all know that when a value is determined, both sides are enclosed by vertical bars. To achieve this, use the vmatrix argument.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[\begin{vmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{vmatrix}\]
\end{document}Output :
Use double vertical bars
You may have noticed that double vertical bars are used on both sides. To achieve this, use Vmatrix as the argument, ensuring that V is capitalized.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[ \begin{Vmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{Vmatrix} \]
\end{document}Output :
If you look at the above programs, you can easily understand which argument is used for which bracket!
Define different types of matrices in LaTeX
The classification is based on the position of the elements within the structure.
Square matrix
In this case, the number of rows and columns must be equal, as it forms a square structure.
\[ \begin{bmatrix}
a_{1,1} & a_{1,2} & \cdots & a_{1,m} \\
a_{2,1} & a_{2,2} & \cdots & a_{2,m} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m,1} & a_{m,2} & \cdots & a_{m,m}
\end{pmatrix} \]Output :
Null matrix
In the case of a zero structure, all elements will be zero.
\[ \begin{bmatrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{bmatrix} \]Output :
Diagonal matrix
The elements of the diagonal matrix are located along the diagonal.
\[ \begin{bmatrix}
a_{1} & & \\
& \ddots & \\
& & a_{n}
\end{bmatrix} \]Output :
Row matrix
In this case, the elements are arranged in a single row.
\[ \begin{pmatrix}
a_{1} & \cdots & a_{n}
\end{pmatrix} \]Output :
Column matrix
In the same way, the elements are located along a column.
\[ \begin{bmatrix}
a_{1} \\ \vdots \\ a_{n}
\end{bmatrix} \]Output :
There are many other types of matrices beyond those mentioned above. Hopefully, with the help of LaTeX, you will be able to represent them in the same way.
Use physics package
You can represent the structure using the physics package instead of amsmath. The \matrixquantity command is used for this purpose, and its shorthand form is \mqty.
Pass the body as an argument in the \mqty command, which consists of a combination of rows and columns. See the example below.
\documentclass{article}
\usepackage{physics}
\begin{document}
\[ \mqty{a & b \\ c & d} \]
\end{document}Output :
You can use different types of brackets on both sides. However, the command syntax varies depending on the bracket type.
\documentclass{article}
\usepackage{physics}
\begin{document}
\[\mqty{a & b \\ c & d}
\quad
\mqty(a & b \\ c & d)
\quad
\mqty*(a & b \\ c & d)
\quad
\mqty[a & b \\ c & d]
\quad
\mqty|a & b \\ c & d| \]
\end{document}Output :

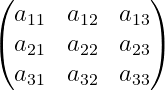
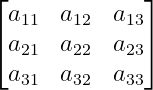
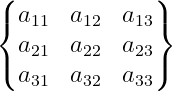
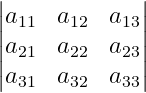
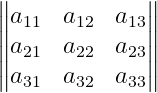
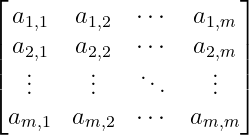
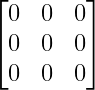
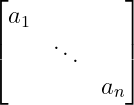
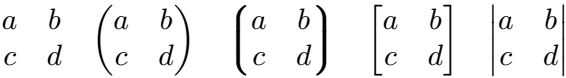
agar hm matrix main matrix k sath numbering dena chahty ho column num or rows ko matrix pa e to wo kaise latix main add ho ga?
kindly plx bta dye.
In the image below, did you want this kind of output? Where the equation number will come with the matrix! Please confirm this ???
