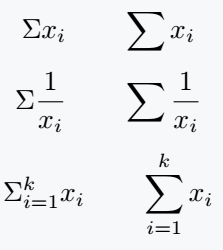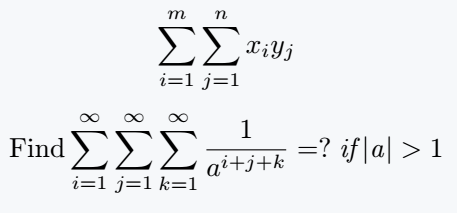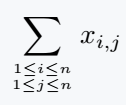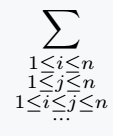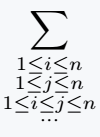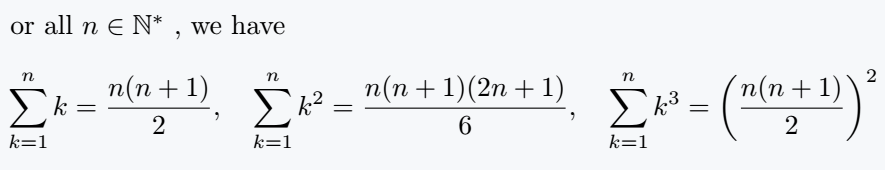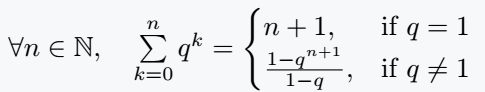LaTeX provides built-in support for summation notation through its default commands and the amsmath package.
This tutorial explores various methods for typesetting summations with practical examples.
In mathematics, summation is represented by the Greek capital letter sigma (∑). In LaTeX, the commands \sum and \Sigma produce this symbol.
However, while \Sigma remains a fixed size, \sum adjusts dynamically based on the surrounding expression.
\documentclass{article}
\begin{document}
\[ \Sigma x_i \qquad \sum x_i \]
\[ \Sigma \frac{1}{x_i} \qquad \sum \frac{1}{x_i} \]
\[ \Sigma_{i=1}^k x_i \qquad \sum_{i=1}^k x_i \]
\end{document}Output :
Summation with Limits
To display summation with limits above and below the symbol in LaTeX, use \sum_{min}^{max}.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
Summation in Mathematics is denoted by the symbol $ \sum $ and for a set of real numbers $ x_1, x_2, \cdots, x_n $, their sum is defined as $ \sum_{k=1}^{n}x_k $ . That is
\[ \sum_{k=1}^{n}x_k = x_1 + x_2 + \cdots + x_{n-1} + x_n \]
\end{document}Output :
Summation sign together with the limits appears differently in the inline mode and display mode.
In inline mode limits appear next to the symbol and in the display mode the limit appear below and above the summation sign.
The are two commands that are capable of controlling how these limits appear.
First is the \limits command which forcefully pushes the limits below and above the summation sign in all the math modes and the second is the \nolimits command which reverse the effect(forces the limits to stay next to the summation symbol in all math modes).
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\begin{center}
\begin{tabular}{|@{\quad}c@{\quad}|@{\quad}c|}
\hline
\multicolumn{2}{|c|}{Summation in math mode} \\
\hline
inline math mode & display math mode \\
$ \sum_{k=1}^n $ & $ {\displaystyle \sum_{k=1}^n} $\\
\hline
\multicolumn{2}{|c|}{Summation in math mode with \color{teal}{\textbackslash{}limits}}\\
\hline
$ \sum\limits_{k=1}^n $ & $ {\displaystyle \sum\limits_{k=1}^{n}} $\\
\hline
\multicolumn{2}{|c|}{Summation in math mode with \color{teal}{\textbackslash{}nolimits} }\\
\hline
$ \sum\nolimits_{k=1}^n $ & $ {\displaystyle \sum\nolimits_{k=1}^{n} }$\\
\hline
\end{tabular}
\end{center}
\end{document}Double and triple sums
You can easily typeset double and triple integrals by using the sum(summation) LaTeX command twice and trice. For example.
\sum\sum = ∑ ∑ and \sum\sum\sum = ∑ ∑ ∑
\documentclass{article}
\begin{document}
\[ \sum\limits_{i=1}^m\sum\limits_{j=1}^n x_i y_j \]
\[ \mathrm{Find} \sum\limits_{i=1}^\infty\sum\limits_{j=1}^\infty\sum\limits_{k=1}^\infty \frac{1}{a^{i+j+k}}=?\;\mathit{if}|\mathit{a}|>1 \]
\end{document}Output :
Use two and multiple subscripts under Sum
1. \atop : This command permit you to write two lines under your sum notation. For example
\documentclass{article}
\begin{document}
\[ \sum_{ 1 \leq i \leq n \atop 1 \leq j \leq n }x_{i,j}\]
\end{document}Output :
2. \substack{argument}: This command permit you to write multiple lines under the sum notation by taking the lines as arguments and breaking them using the newline command \\. For example
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[ \sum_{\substack{ 1 \leq i \leq n \\ 1 \leq j \leq n \\ 1 \leq i \leq j \leq n\\ \cdots }} \]
\end{document}Output :
3. \begin{subarray}{column_definition} \cdots \end{subarray}: This environment permits you to achieve the same effect as \substack{argument}. For example:
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[ \sum_{\begin{subarray}{c}
1 \leq i \leq n \\
1 \leq j \leq n \\
1 \leq i \leq j \leq n\\
\cdots \\
\end{subarray} } \]
\end{document}Output :
4. \sideset{left}{right}{symbol} makes it possible for you to place a number or a symbol at all four corners of the sum symbol.
It enables the placement of characters that cannot be positioned using limits, such as a prime before the summation symbol. For example:
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[ \sideset{_{\alpha}
^{\beta}}
{_{\gamma}
^{\sigma}}\sum_{ 1 \leq i \leq n \atop 1 \leq j \leq n }x_{i,j} \]
adding a prime to the sum
\[ \sideset{}{'}\sum_{ 1 \leq i \leq n \atop 1 \leq j \leq n }x_{i,j} \]
\end{document}Output :
Some examples
As you can easily understand, the sum symbol is used in the following different types of mathematical expressions.
\documentclass{article}
\usepackage{amssymb}
\begin{document}
or all $ n \in \mathbb{N}^{\ast} $ , we have
\[ \sum_{k=1}^{n}k = \frac{n(n+1)}{2}, \quad \sum_{k=1}^{n}k^2 = \frac{n(n+1)(2n+1)}{6}, \quad \sum_{k=1}^{n}k^3 = \left(\frac{n(n+1)}{2}\right)^2 \]
\end{document}Output :
Geometric sum
\documentclass{article}
\usepackage{amssymb,amsmath}
\begin{document}
$ \forall n \in \mathbb{N}, \quad \sum\limits_{k=0}^{n}q^k =\begin{cases}
n + 1, & \text{if $ q = 1 $}\\
\frac{1-q^{n+1}}{1-q}, & \text{if $ q \neq 1 $}
\end{cases} $
\end{document}Output :
\documentclass{article}
\usepackage{amsmath}
\begin{document}
Interchanging double sums when the indices are dependent
\[ \sum_{1 \leq i \leq j \leq n}x_{i,j} = \sum_{i = 1}^{n}\sum_{j=1}^{n}x_{i,j} = \sum_{ j = 1}^{n}\sum_{i=1}^{j}x_{i,j} \; \text{and}\;
\sum_{1 \leq i \leq j \leq n}x_{i,j} = \sum_{i=1}^{n-1}\sum_{j = i+1}x_{i,j} = \sum_{j=2}^{n}\sum_{i=1}^{j-1}x_{i,j} \]
Commutativity and associativity property of double sums
\[ \sum_{k \leq j \leq i \leq n}a_{ij} = \sum_{i=k}^{n}\sum_{j=k}^{i}a_{i,j} = \sum_{j=k}^{n}\sum_{i=j}^{n}a_{ij} = \sum_{j=0}^{n-k}\sum_{i=k}^{n-j}a_{i+j,i} \]
\end{document}Output :
Conclusion
This article gives you a full coverage of how to typeset summations in LaTeX and some few related commands.
A good mastery of this tutorial will improve your mathematical typesetting and make you an efficient typesetter of higher mathematics.